Competing with C++ with Julia in multithreaded, allocating code
#Benchmarking test case
Our benchmark test case will be applying ForwardMode AD with dual numbers with dynamically sized square matrices of size 2x2...8x8 on multiple threads. We'll test no duals, and dual sizes 1:8 for single derivatives, and 1:8 by 1:2 for second derivatives. This gives us a large number of combinations, which increases the working memory we need a bit. We'll iterate over a range of scale factors, to hit different code-paths based on the op-norm of the matrices. For each scale factor, we'll iterate over all tested matrices to increase the working set of memory, to simulate more realistic workloads that may (for example) be solving a large number of affine differential equations as part of an optimization problem. For Julia, we'll be using ForwardDiff.jl, and for C++ we use an implementation from the LoopModels supporting math library.
The function we're benchmarking:
using Base.Threads
#utilities for dealing with nested tuples
#we use nested instead of flat tuples to avoid heuristics
#that avoid specializing on long tuples
rmap(f, ::Tuple{}) = ()
rmap(f::F, x::Tuple) where {F} = map(f, x)
rmap(f::F, x::Tuple{Vararg{Tuple,K}}) where {F,K} = map(Base.Fix1(rmap, f), x)
rmap(f, ::Tuple{}, ::Tuple{}) = ()
rmap(f::F, x::Tuple, y::Tuple) where {F} = map(f, x, y)
rmap(f::F, x::Tuple{Vararg{Tuple,K}}, y::Tuple{Vararg{Tuple,K}}) where {F,K} = map((a,b)->rmap(f,a,b), x, y)
#rmaptnum applies `f` to a tuple of non - tuples
rmaptnum(f, ::Tuple{}) = ()
rmaptnum(f::F, x::Tuple{Vararg{Tuple{Vararg}}}) where {F} = map(f, x)
rmaptnum(f::F, x::Tuple{Vararg{Tuple{Vararg{Tuple}}}}) where {F} = map(Base.Fix1(rmaptnum,f), x)
struct SumScaleMatrixExponential{F}
f!::F
s::Float64
end
function (sme::SumScaleMatrixExponential)(B, A)
for i in eachindex(B, A)
B[i] = sme.s * A[i]
end
sme.f!(B)
return sum(B)
end
function do_singlethreaded_work!(f!::F, Bs, As, r) where {F}
ret = rmaptnum(zero ∘ eltype ∘ eltype, Bs)
for s in r
incr = rmap(SumScaleMatrixExponential(f!, s), Bs, As)
ret = rmap(+, ret, rmaptnum(sum,incr))
end
return ret
end
function do_multithreaded_work!(f!::F, Bs, As, r) where {F}
nt = Threads.nthreads(:default)
nt > 1 || return do_singlethreaded_work!(f!, Bs, As, r)
tasks = Vector{Task}(undef, nt)
for n in 1:nt
subrange = r[n:nt:end] # stride to balance opnorms across threads
Bsc = n == nt ? Bs : rmap(copy, Bs)
tasks[n] = Threads.@spawn do_singlethreaded_work!($f!, $Bsc, $As, $subrange)
end
_ret = rmaptnum(zero ∘ eltype ∘ eltype, Bs)
ret::typeof(_ret) = Threads.fetch(tasks[1])
for n in 2:nt
ret = rmap(+, ret, Threads.fetch(tasks[n]))
end
return ret
end;We need some boiler plate to deal with large numbers of different types in stable manner by iterating over tuples. The code calculates a matrix exponential after scaling an input, and accumulates a sum of the results. Lets create some test case matrices:
using ForwardDiff
d(x, n) = ForwardDiff.Dual(x, ntuple(_->randn(), n))
function dualify(A, n, j)
n == 0 && return A
j == 0 ? d.(A, n) : d.(d.(A, n), j)
end
randdual(n, dinner, douter) = dualify(rand(n, n), dinner, douter)
max_size = 5;
As = map((0, 1, 2)) do dout #outer dual
map( ntuple(identity, Val(9)) .- 1) do din #inner dual
map(ntuple(identity, Val(max_size - 1)) .+ 1) do n #matrix size
randdual(n, din, dout)
end
end
end;
Bs = rmap(similar, As);Lets set C++ as a baseline with this.We'll base our implementation on StaticArrays.exp, as this implementation is simpler than the one from ExponentialUtilities.jl. The core of our C++ implementation is only 50 lines of code:
template <typename T> constexpr void expm(MutSquarePtrMatrix<T> A) {
ptrdiff_t n = ptrdiff_t(A.numRow()), s = 0;
SquareMatrix<T> A2{SquareDims<>{{n}}}, U_{SquareDims<>{{n}}};
MutSquarePtrMatrix<T> U{U_};
if (double nA = opnorm1(A); nA <= 0.015) {
A2 << A * A;
U << A * (A2 + 60.0 * I);
A << 12.0 * A2 + 120.0 * I;
} else {
SquareMatrix<T> B{SquareDims<>{{n}}};
if (nA <= 2.1) {
A2 << A * A;
containers::TinyVector<double, 5> p0, p1;
if (nA > 0.95) {
p0 = {1.0, 3960.0, 2162160.0, 302702400.0, 8821612800.0};
p1 = {90.0, 110880.0, 3.027024e7, 2.0756736e9, 1.76432256e10};
} else if (nA > 0.25) {
p0 = {1.0, 1512.0, 277200.0, 8.64864e6};
p1 = {56.0, 25200.0, 1.99584e6, 1.729728e7};
} else {
p0 = {1.0, 420.0, 15120.0};
p1 = {30.0, 3360.0, 30240.0};
}
evalpoly(B, U, A2, p0);
U << A * B;
evalpoly(A, B, A2, p1);
} else {
// s = std::max(unsigned(std::ceil(std::log2(nA / 5.4))), 0);
s = nA > 5.4 ? log2ceil(nA / 5.4) : 0;
if (s & 1) { // we'll swap `U` and `A` an odd number of times
std::swap(A, U); // so let them switch places
A << U * exp2(-s);
} else if (s > 0) A *= exp2(-s);
A2 << A * A;
// here we take an estrin (instead of horner) approach to cut down flops
SquareMatrix<T> A4{A2 * A2}, A6{A2 * A4};
B << A6 * (A6 + 16380 * A4 + 40840800 * A2) +
(33522128640 * A6 + 10559470521600 * A4 + 1187353796428800 * A2) +
32382376266240000 * I;
U << A * B;
A << A6 * (182 * A6 + 960960 * A4 + 1323241920 * A2) +
(670442572800 * A6 + 129060195264000 * A4 +
7771770303897600 * A2) +
64764752532480000 * I;
}
}
containers::tie(A, U) << containers::Tuple(A + U, A - U);
LU::ldiv(U, MutPtrMatrix<T>(A));
for (; s--; std::swap(A, U)) U << A * A;
}Now, to compile it
withenv("CXX" => "clang++") do
@time run(`cmake -S . -B buildclang -DCMAKE_BUILD_TYPE=Release -DCMAKE_UNITY_BUILD=ON`)
end
withenv("CXX" => "g++") do
@time run(`cmake -S . -B buildgcc -DCMAKE_BUILD_TYPE=Release -DCMAKE_UNITY_BUILD=ON`)
end
@time run(`cmake --build buildclang`);
@time run(`cmake --build buildgcc`);-- The CXX compiler identification is Clang 17.0.5
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /bin/clang++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-- CPM: Adding package PackageProject.cmake@1.8.0 (v1.8.0 at /home/chriselr
od/.cache/CPM/packageproject.cmake/987b02f8a9fe04de3c43e0e7a1afbb29c87adc5e
)
-- Using 2 batch size
-- Configuring done (1.2s)
-- Generating done (0.0s)
-- Build files have been written to: /home/chriselrod/Documents/progwork/cx
x/MatrixExp/buildclang
1.208517 seconds (157 allocations: 204.523 KiB)
-- The CXX compiler identification is GNU 13.2.1
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /bin/g++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-- CPM: Adding package PackageProject.cmake@1.8.0 (v1.8.0 at /home/chriselr
od/.cache/CPM/packageproject.cmake/987b02f8a9fe04de3c43e0e7a1afbb29c87adc5e
)
-- Using 2 batch size
-- Configuring done (1.1s)
-- Generating done (0.0s)
-- Build files have been written to: /home/chriselrod/Documents/progwork/cx
x/MatrixExp/buildgcc
1.078525 seconds (154 allocations: 3.977 KiB)
[ 0%] Built target Math
[ 7%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_12_cxx.cxx.
o
[ 14%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_11_cxx.cxx.
o
[ 21%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_10_cxx.cxx.
o
[ 28%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_9_cxx.cxx.o
[ 35%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_8_cxx.cxx.o
[ 42%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_7_cxx.cxx.o
[ 50%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_6_cxx.cxx.o
[ 57%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_5_cxx.cxx.o
[ 64%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_4_cxx.cxx.o
[ 71%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_3_cxx.cxx.o
[ 78%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_2_cxx.cxx.o
[ 85%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_1_cxx.cxx.o
[ 92%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_0_cxx.cxx.o
[100%] Linking CXX shared library libMatrixExp.so
[100%] Built target MatrixExp
4.544968 seconds (191 allocations: 4.391 KiB)
[ 0%] Built target Math
[ 7%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_12_cxx.cxx.
o
[ 14%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_11_cxx.cxx.
o
[ 21%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_9_cxx.cxx.o
[ 28%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_10_cxx.cxx.
o
[ 35%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_8_cxx.cxx.o
[ 42%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_7_cxx.cxx.o
[ 50%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_6_cxx.cxx.o
[ 57%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_5_cxx.cxx.o
[ 64%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_4_cxx.cxx.o
[ 71%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_3_cxx.cxx.o
[ 78%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_2_cxx.cxx.o
[ 85%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_1_cxx.cxx.o
[ 92%] Building CXX object CMakeFiles/MatrixExp.dir/Unity/unity_0_cxx.cxx.o
[100%] Linking CXX shared library libMatrixExp.so
[100%] Built target MatrixExp
4.321814 seconds (191 allocations: 4.391 KiB)This compiled all combinations we need; lets wrap them so we can call them.
const libExpMatGCC = joinpath(@__DIR__, "buildgcc/libMatrixExp.so")
const libExpMatClang = joinpath(@__DIR__, "buildclang/libMatrixExp.so")
for (lib, cc) in ((:libExpMatGCC, :gcc), (:libExpMatClang, :clang))
j = Symbol(cc, :expm!)
@eval $j(A::Matrix{Float64}) =
@ccall $lib.expmf64(A::Ptr{Float64}, size(A, 1)::Clong)::Nothing
for n = 1:8
sym = Symbol(:expmf64d, n)
@eval $j(A::Matrix{ForwardDiff.Dual{T,Float64,$n}}) where {T} =
@ccall $lib.$sym(A::Ptr{Float64}, size(A, 1)::Clong)::Nothing
for i = 1:2
sym = Symbol(:expmf64d, n, :d, i)
@eval $j(
A::Matrix{ForwardDiff.Dual{T1,ForwardDiff.Dual{T0,Float64,$n},$i}}
) where {T0,T1} =
@ccall $lib.$sym(A::Ptr{Float64}, size(A, 1)::Clong)::Nothing
end
end
endSo, now, let's set clang as baseline (as it uses LLVM, like Julia):
testrange = range(0.001, stop = 6.0, length=1<<16);
resclang = @time @eval do_multithreaded_work!(clangexpm!, Bs, As, testrange);
GC.gc();
t_clang = @elapsed do_multithreaded_work!(clangexpm!, Bs, As, testrange);
resgcc = @time @eval do_multithreaded_work!(gccexpm!, Bs, As, testrange);
GC.gc();
t_gcc = @elapsed do_multithreaded_work!(gccexpm!, Bs, As, testrange);
@show t_clang t_gcc;3.877563 seconds (6.26 M allocations: 1.283 GiB, 3.41% gc time, 2427.35% compilation time)
1.582645 seconds (827.49 k allocations: 967.367 MiB, 2.70% gc time, 1280.43% compilation time)
t_clang = 0.796717248
t_gcc = 0.879461508Great, now for our Julia implementations. While we'll also base our Julia code on this implemtantion, to start with we'll first try ExponentialUtilities.jl to see how it compares. ExponentialUtilities.exponential! is likely what most people will reach for once they find that Base.exp(::AbstractMatrix) doesn't support ForwardDiff.Dual numbers:
using ForwardDiff, Test
A = rand(4, 4)
@test_throws MethodError ForwardDiff.gradient(sum∘exp, A)
using ExponentialUtilities
ForwardDiff.gradient(sum∘exponential!∘copy, A);
#no throwIt could be this just works great and we can go home / end the blog post early. =) So, let's see how it compares.
res = @time do_multithreaded_work!(exponential!, Bs, As, testrange);
GC.gc();
t_exputils = @elapsed do_multithreaded_work!(exponential!, Bs, As, testrange);
@show t_exputils;193.872166 seconds (320.69 M allocations: 461.891 GiB, 11.27% gc time, 3223.70% compilation time)
t_exputils = 18.912085601Oof – compare both that compile time, and the runtime!
Lets confirm that our answers match.
approxd(x, y) = isapprox(x, y)
function approxd(x::ForwardDiff.Dual, y::ForwardDiff.Dual)
approxd(x.value, y.value) && approxd(Tuple(x.partials), Tuple(y.partials))
end
approxd(x::Tuple, y::Tuple) = all(map(approxd, x, y))
@test approxd(res, resclang)Test Passed@test approxd(res, resgcc)Test PassedGreat. Now, let's visualize where we stand in terms of performance.
using CairoMakie
function cmpplot(labels, times)
f = Figure()
ax = Axis(f[1,1],
title = "Relative Runtime",
xticks=(eachindex(labels), labels)
)
barplot!(ax, eachindex(times), times)
hlines!(ax, [1])
f
end
cmpplot(["Clang", "GCC", "ExponentialUtilities.jl"], [1.0, t_gcc/t_clang, t_exputils/t_clang])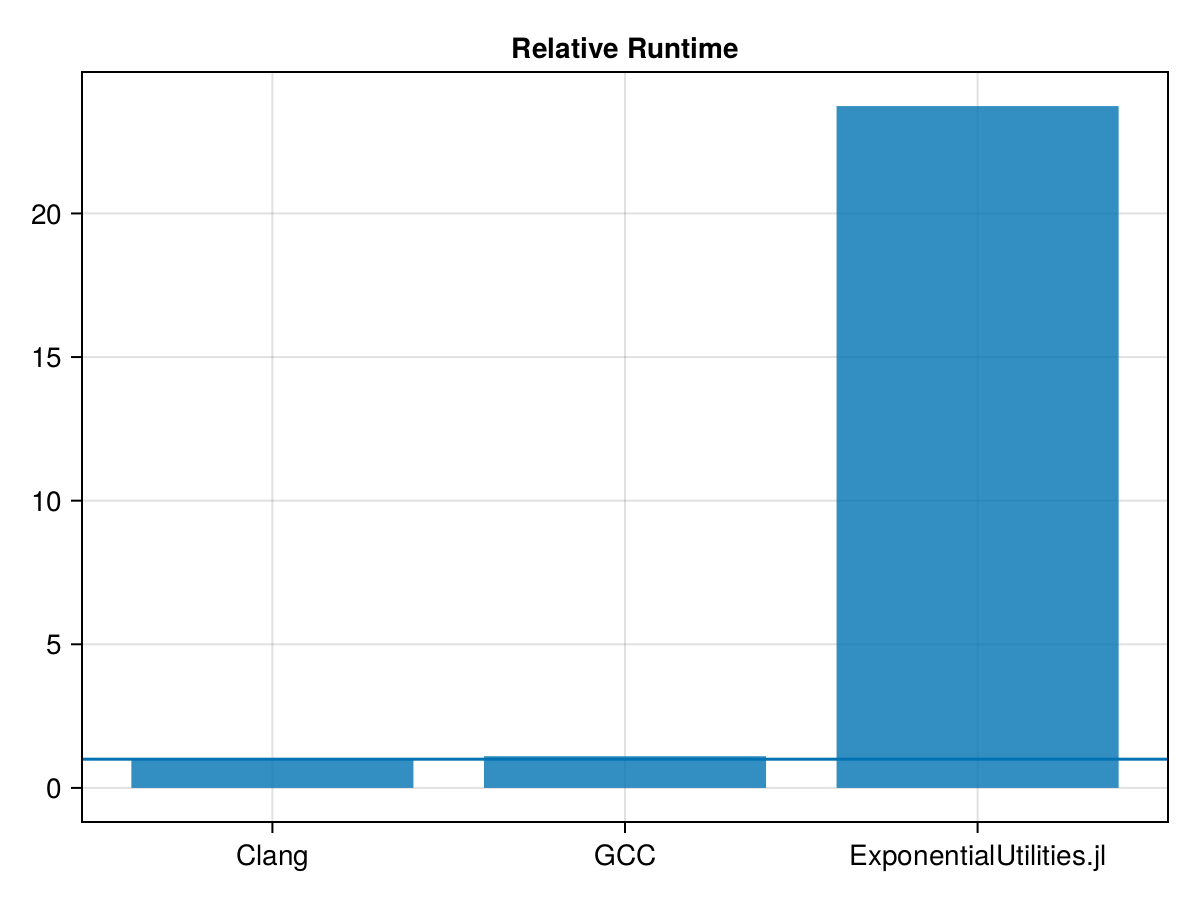
Okay, lets try a Julia implementation mirroring our C++ code.
using LinearAlgebra
#My C++ `opnorm` implementation only looks at Dual's values
#so lets just go ahead and copy that optimization here.
_deval(x) = x
_deval(x::ForwardDiff.Dual) = _deval(ForwardDiff.value(x))
function opnorm1(A)
n = _deval(zero(eltype(A)))
@inbounds for j in axes(A, 2)
s = _deval(zero(eltype(A)))
@simd for i in axes(A, 1)
s += abs(_deval(A[i, j]))
end
n = max(n, s)
end
return n
end
#Let's also immediately implement our own `evalpoly` to cut down
#allocations. `B` contains the result, `A` is a temporary
#that we reuse(following the same approach as in C++)
function matevalpoly!(B, A, C, t::NTuple, N)
@assert N > 1
if isodd(N)
A, B = B, A
end
B .= t[1] .* C
@view(B[diagind(B)]) .+= t[2]
for n in 3:N
A, B = B, A
mul!(B, A, C)
@view(B[diagind(B)]) .+= t[n]
end
end
log2ceil(x::Float64) =
(reinterpret(Int, x) - 1) >> Base.significand_bits(Float64) - 1022
function expm!(A::AbstractMatrix)
N = size(A, 1)
s = 0
N == size(A, 2) || error("Matrix is not square.")
A2 = similar(A)
U = similar(A)
if (nA = opnorm1(A); nA <= 0.015)
mul!(A2, A, A)
mul!(U, A, A2 + 60.0I) # broadcasting doesn't work with `I`
A .= 12.0 .* A2
@view(A[diagind(A)]) .+= 120.0
else
B = similar(A)
if nA <= 2.1 #No need to specialize on different tuple sizes
mul!(A2, A, A)
if nA > 0.95
p0 = (1.0, 3960.0, 2162160.0, 302702400.0, 8821612800.0)
p1 = (90.0, 110880.0, 3.027024e7, 2.0756736e9, 1.76432256e10)
N = 5
elseif nA > 0.25
p0 = (1.0, 1512.0, 277200.0, 8.64864e6, 0.0)
p1 = (56.0, 25200.0, 1.99584e6, 1.729728e7, 0.0)
N = 4
else
p0 = (1.0, 420.0, 15120.0, 0.0, 0.0)
p1 = (30.0, 3360.0, 30240.0, 0.0, 0.0)
N = 3
end
matevalpoly!(B, U, A2, p0, N)
mul!(U, A, B)
matevalpoly!(A, B, A2, p1, N)
else
s = nA > 5.4 ? log2ceil(nA / 5.4) : 0
if isodd(s) # need to swap
A, U = U, A # as we have an odd number of swaps at the end
A .= U .* exp2(-s)
elseif s > 0
A .*= exp2(-s)
end
mul!(A2, A, A)
A4 = A2 * A2
A6 = A2 * A4
#we use `U` as a temporary here that we didn't
#need in the C++ code for the estrin - style polynomial
#evaluation.Thankfully we don't need another allocation!
@. U = A6 + 16380 * A4 + 40840800 * A2
mul!(B, A6, U)
@. B += 33522128640 * A6 + 10559470521600 * A4 + 1187353796428800 * A2
@view(B[diagind(B)]) .+= 32382376266240000
mul!(U, A, B)
# `A` being filled by the answer
#we use `B` as a temporary here we didn't
#need in the C++ code
@. B = 182 * A6 + 960960 * A4 + 1323241920 * A2
mul!(A, A6, B)
@. A += 670442572800 * A6 + 129060195264000 * A4 +
7771770303897600 * A2
@view(A[diagind(A)]) .+= 64764752532480000
end
end
@inbounds for i = eachindex(A, U)
A[i], U[i] = A[i] + U[i], A[i] - U[i]
end
ldiv!(lu!(U), A)
for _ in 1:s
mul!(U, A, A)
A, U = U, A
end
end;This should do roughly the same thing; does it help ?
resexpm = @time @eval do_multithreaded_work!(expm!, Bs, As, testrange);
@test approxd(res, resexpm)
GC.gc();
t_expm = @elapsed do_multithreaded_work!(expm!, Bs, As, testrange)
@show t_expm;
cmpplot(
["Clang", "GCC", "ExponentialUtilities.jl", "expm!"],
[1.0, t_gcc/t_clang, t_exputils/t_clang, t_expm/t_clang]
)48.529428 seconds (175.40 M allocations: 465.740 GiB, 35.11% gc time, 2093.19% compilation time)
t_expm = 19.342165029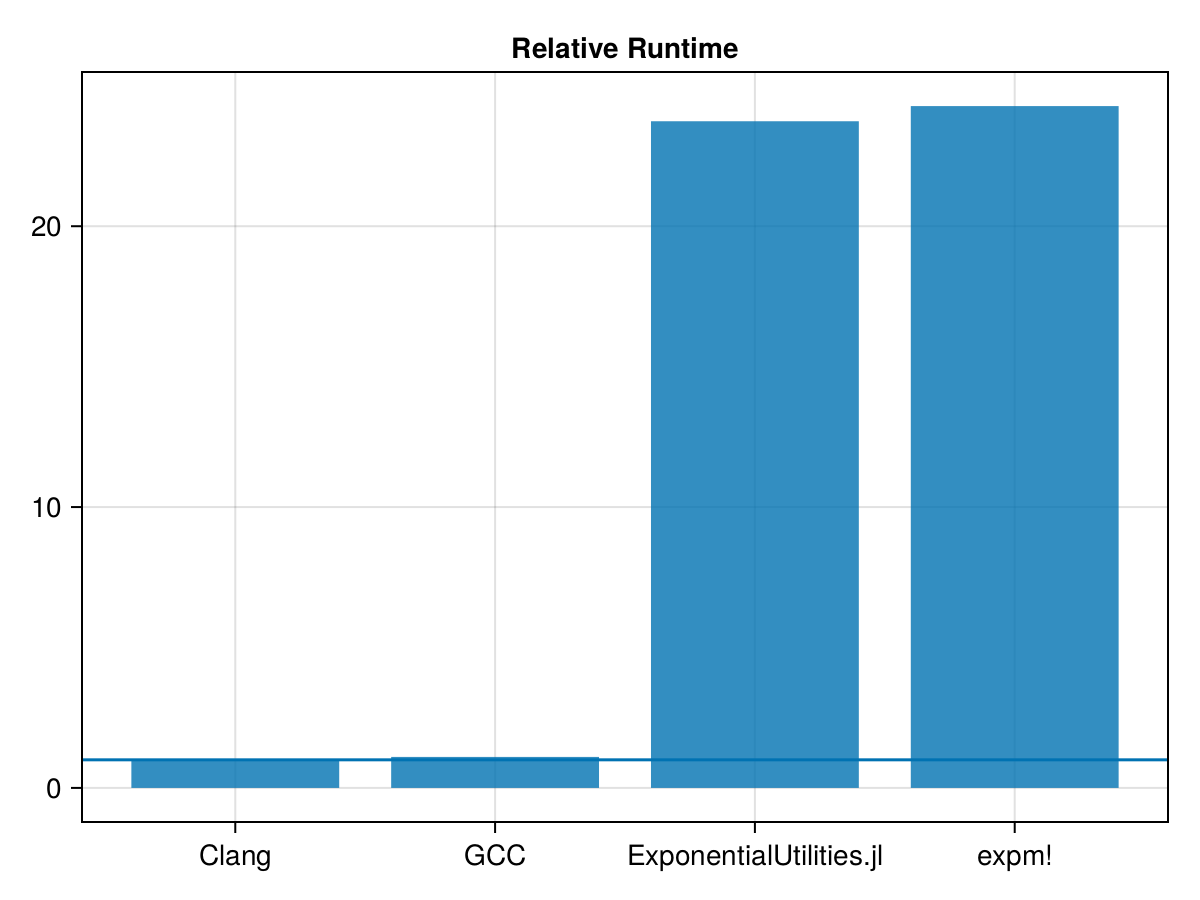
No, not really. One of the major issues is that mul! is extremely slow for ForwardDiff.Dual numbers. Julia PR#52038 will help immensely. However, it'll only be in Julia 1.11, and we're currently still on the latest release, Julia 1.9.4. So let's implement the newer matrix multiply method here.
function mulreduceinnerloop!(C, A, B)
AxM = axes(A, 1)
AxK = axes(A, 2) # we use two `axes` calls in case of `AbstractVector`
BxK = axes(B, 1)
BxN = axes(B, 2)
CxM = axes(C, 1)
CxN = axes(C, 2)
if AxM != CxM
throw(DimensionMismatch(lazy"matrix A has axes ($AxM,$AxK), matrix C has axes ($CxM,$CxN)"))
end
if AxK != BxK
throw(DimensionMismatch(lazy"matrix A has axes ($AxM,$AxK), matrix B has axes ($BxK,$CxN)"))
end
if BxN != CxN
throw(DimensionMismatch(lazy"matrix B has axes ($BxK,$BxN), matrix C has axes ($CxM,$CxN)"))
end
@inbounds for n = BxN, m = AxM
Cmn = zero(eltype(C))
for k = BxK
Cmn = muladd(A[m,k], B[k,n], Cmn)
end
C[m,n] = Cmn
end
return C
end
function matevalpoly_custommul!(B, A, C, t::NTuple, N)
@assert N > 1
if isodd(N)
A, B = B, A
end
B .= t[1] .* C
@view(B[diagind(B)]) .+= t[2]
for n in 3:N
A, B = B, A
mulreduceinnerloop!(B, A, C)
@view(B[diagind(B)]) .+= t[n]
end
end
function expm_custommul!(A::AbstractMatrix)
N = size(A, 1)
s = 0
N == size(A, 2) || error("Matrix is not square.")
A2 = similar(A)
U = similar(A)
if (nA = opnorm1(A); nA <= 0.015)
mulreduceinnerloop!(A2, A, A)
mulreduceinnerloop!(U, A, A2 + 60.0I)
#broadcasting doesn't work with `I`
A .= 12.0 .* A2
@view(A[diagind(A)]) .+= 120.0
else
B = similar(A)
if nA <= 2.1
mulreduceinnerloop!(A2, A, A)
#No need to specialize on different tuple sizes
if nA > 0.95
p0 = (1.0, 3960.0, 2162160.0, 302702400.0, 8821612800.0)
p1 = (90.0, 110880.0, 3.027024e7, 2.0756736e9, 1.76432256e10)
N = 5
elseif nA > 0.25
p0 = (1.0, 1512.0, 277200.0, 8.64864e6, 0.0)
p1 = (56.0, 25200.0, 1.99584e6, 1.729728e7, 0.0)
N = 4
else
p0 = (1.0, 420.0, 15120.0, 0.0, 0.0)
p1 = (30.0, 3360.0, 30240.0, 0.0, 0.0)
N = 3
end
matevalpoly_custommul!(B, U, A2, p0, N)
mulreduceinnerloop!(U, A, B)
matevalpoly_custommul!(A, B, A2, p1, N)
else
s = nA > 5.4 ? log2ceil(nA / 5.4) : 0
if isodd(s) # need to swap
A, U = U, A # as we have an odd number of swaps at the end
A .= U .* exp2(-s)
elseif s > 0
A .*= exp2(-s)
end
mulreduceinnerloop!(A2, A, A)
A4 = mulreduceinnerloop!(similar(A), A2, A2)
A6 = mulreduceinnerloop!(similar(A), A2, A4)
#we use `U` as a temporary here that we didn't
#need in the C++ code for the estrin - style polynomial
#evaluation.Thankfully we don't need another allocation!
@. U = A6 + 16380 * A4 + 40840800 * A2
mulreduceinnerloop!(B, A6, U)
@. B += 33522128640 * A6 + 10559470521600 * A4 + 1187353796428800 * A2
@view(B[diagind(B)]) .+= 32382376266240000
mulreduceinnerloop!(U, A, B)
#Like in the C++ code, we swap A and U `s` times at the end
#so if `s` is odd, we pre - swap to end with the original
# `A` being filled by the answer
#we use `B` as a temporary here we didn't
#need in the C++ code
@. B = 182 * A6 + 960960 * A4 + 1323241920 * A2
mulreduceinnerloop!(A, A6, B)
@. A += 670442572800 * A6 + 129060195264000 * A4 +
7771770303897600 * A2
@view(A[diagind(A)]) .+= 64764752532480000
end
end
@inbounds for i = eachindex(A, U)
A[i], U[i] = A[i] + U[i], A[i] - U[i]
end
ldiv!(lu!(U), A)
for _ in 1:s
mulreduceinnerloop!(U, A, A)
A, U = U, A
end
end
#Testing and timing:
resexpmcm = @time @eval do_multithreaded_work!(expm_custommul!, Bs, As, testrange);
@test approxd(res, resexpmcm)
GC.gc(); t_expm_custommul = @elapsed do_multithreaded_work!(expm_custommul!, Bs, As, testrange)
@show t_expm_custommul
cmpplot(
["Clang", "GCC", "ExponentialUtilities.jl", "expm!", "expm_custommul!"],
[t_clang, t_gcc, t_exputils, t_expm, t_expm_custommul] ./ t_clang
)24.993893 seconds (109.88 M allocations: 41.061 GiB, 20.61% gc time, 2622.92% compilation time)
t_expm_custommul = 6.679263822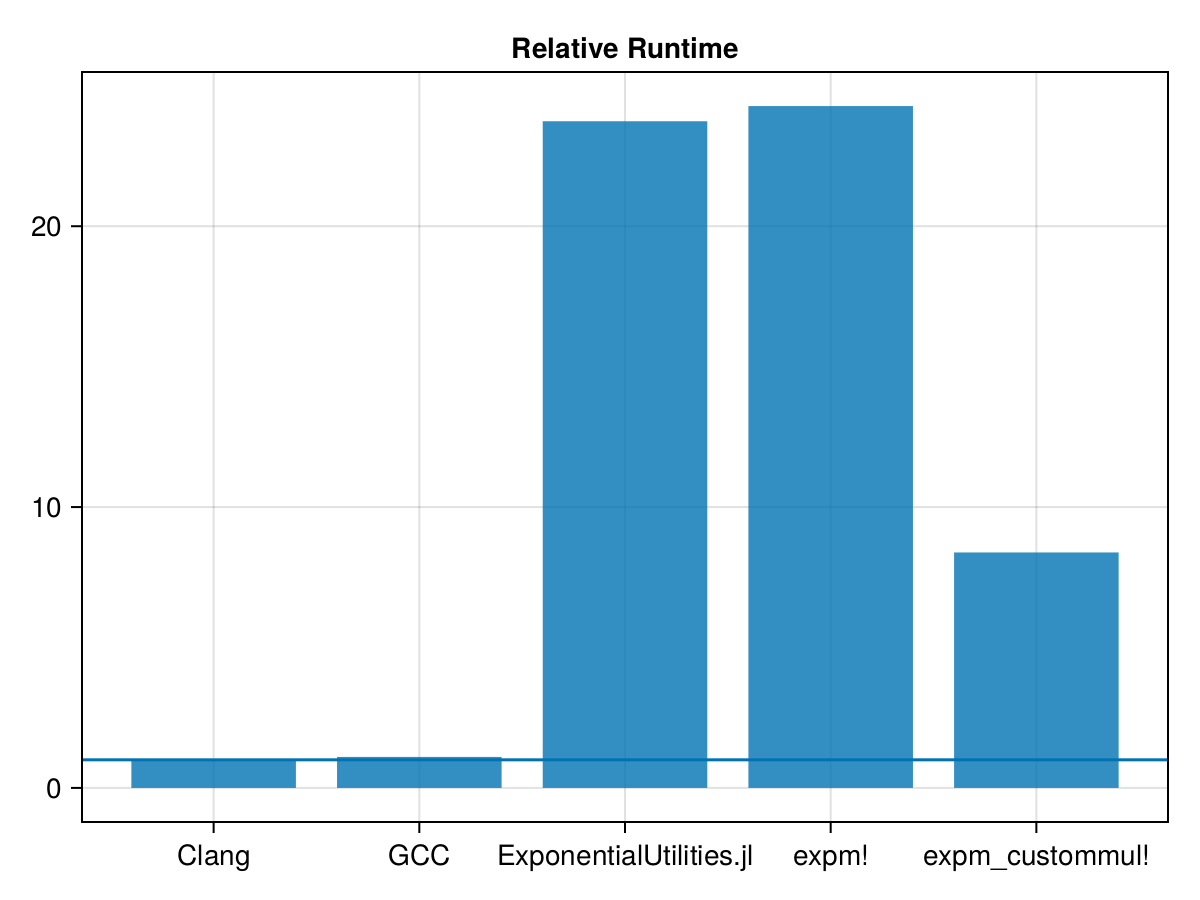
That does help a lot! But we're still well behind.
Timing shows we're spending a lot of time in GC:
@time do_multithreaded_work!(expm_custommul!, Bs, As, testrange);6.677727 seconds (81.55 M allocations: 39.207 GiB, 54.89% gc time)So lets try re-using the same memory through caching preallocations in the task local storage.
function tlssimilar(A)
ret = get!(task_local_storage(), A) do
ntuple(_->similar(A), Val(5))
end
return ret::NTuple{5,typeof(A)}
end
function expm_tls!(A::AbstractMatrix)
N = size(A, 1)
s = 0
N == size(A, 2) || error("Matrix is not square.")
U, B, A2, A4, A6 = tlssimilar(A)
if (nA = opnorm1(A); nA <= 0.015)
mulreduceinnerloop!(A2, A, A)
B .= A2
@view(B[diagind(B)]) .+= 60.0
mulreduceinnerloop!(U, A, B)
#broadcasting doesn't work with `I`
A .= 12.0 .* A2
@view(A[diagind(A)]) .+= 120.0
else
if nA <= 2.1
mulreduceinnerloop!(A2, A, A)
#No need to specialize on different tuple sizes
if nA > 0.95
p0 = (1.0, 3960.0, 2162160.0, 302702400.0, 8821612800.0)
p1 = (90.0, 110880.0, 3.027024e7, 2.0756736e9, 1.76432256e10)
N = 5
elseif nA > 0.25
p0 = (1.0, 1512.0, 277200.0, 8.64864e6, 0.0)
p1 = (56.0, 25200.0, 1.99584e6, 1.729728e7, 0.0)
N = 4
else
p0 = (1.0, 420.0, 15120.0, 0.0, 0.0)
p1 = (30.0, 3360.0, 30240.0, 0.0, 0.0)
N = 3
end
matevalpoly_custommul!(B, U, A2, p0, N)
mulreduceinnerloop!(U, A, B)
matevalpoly_custommul!(A, B, A2, p1, N)
else
s = nA > 5.4 ? log2ceil(nA / 5.4) : 0
if isodd(s) # need to swap
A, U = U, A # as we have an odd number of swaps at the end
A .= U .* exp2(-s)
elseif s > 0
A .*= exp2(-s)
end
mulreduceinnerloop!(A2, A, A)
mulreduceinnerloop!(A4, A2, A2)
mulreduceinnerloop!(A6, A2, A4)
#we use `U` as a temporary here that we didn't
#need in the C++ code for the estrin - style polynomial
#evaluation.Thankfully we don't need another allocation!
@. U = A6 + 16380 * A4 + 40840800 * A2
mulreduceinnerloop!(B, A6, U)
@. B += 33522128640 * A6 + 10559470521600 * A4 + 1187353796428800 * A2
@view(B[diagind(B)]) .+= 32382376266240000
mulreduceinnerloop!(U, A, B)
#Like in the C++ code, we swap A and U `s` times at the end
#so if `s` is odd, we pre - swap to end with the original
# `A` being filled by the answer
#we use `B` as a temporary here we didn't
#need in the C++ code
@. B = 182 * A6 + 960960 * A4 + 1323241920 * A2
mulreduceinnerloop!(A, A6, B)
@. A += 670442572800 * A6 + 129060195264000 * A4 +
7771770303897600 * A2
@view(A[diagind(A)]) .+= 64764752532480000
end
end
@inbounds for i = eachindex(A, U)
A[i], U[i] = A[i] + U[i], A[i] - U[i]
end
ldiv!(lu!(U), A)
for _ in 1:s
mulreduceinnerloop!(U, A, A)
A, U = U, A
end
end
restls = @time @eval do_multithreaded_work!(expm_tls!, Bs, As, testrange)
@test approxd(res, restls)
GC.gc(); t_tls = @elapsed do_multithreaded_work!(expm_tls!, Bs, As, testrange)
@show t_tls
cmpplot(
["Clang", "GCC", "ExponentialUtilities.jl", "expm!", "expm_custommul!", "expm_tls!"],
[t_clang, t_gcc, t_exputils, t_expm, t_expm_custommul, t_tls] ./ t_clang
)20.617839 seconds (78.17 M allocations: 4.970 GiB, 10.37% gc time, 3054.54% compilation time)
t_tls = 2.974135336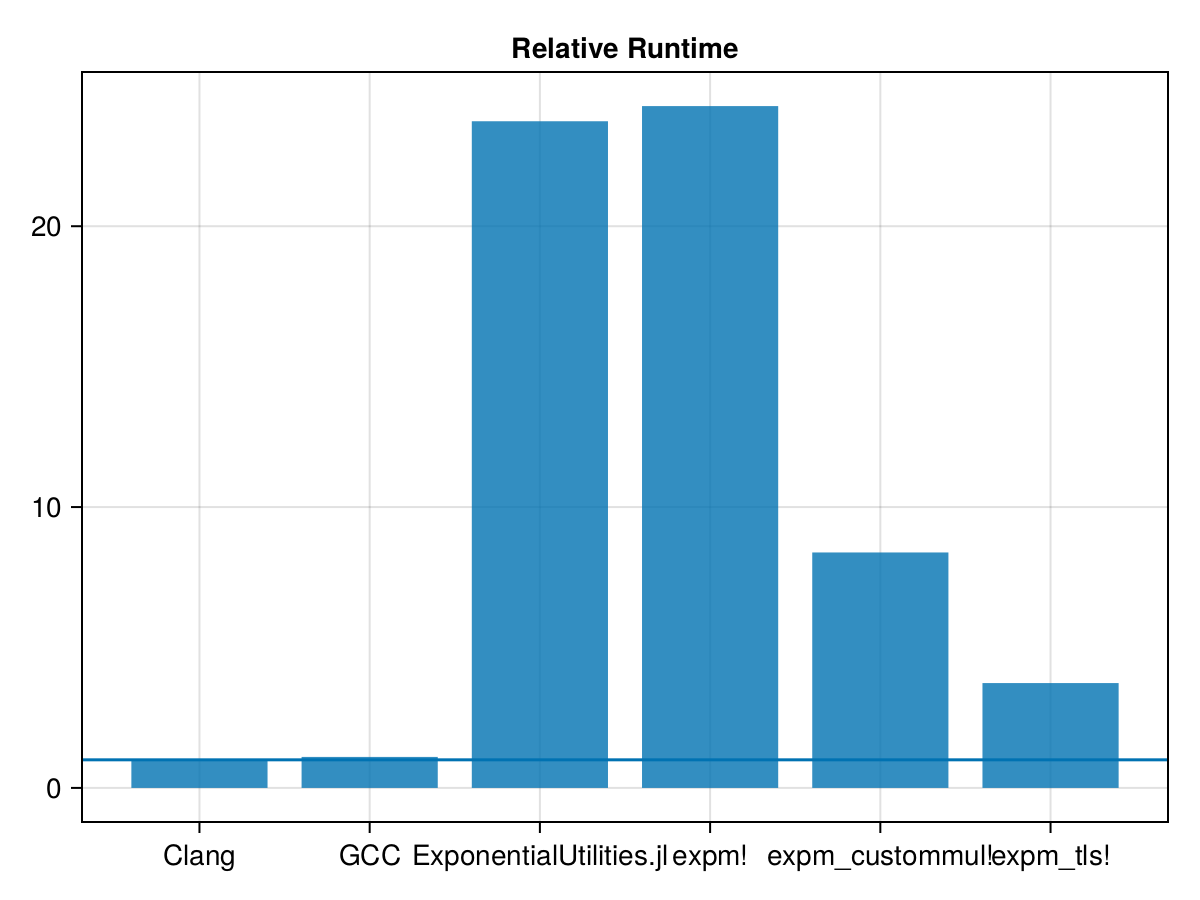
That helps a lot! Note
(t_expm_custommul - t_tls) / t_clang4.650493629077301The total amount of time we saved from this approach is over 4x the total time C++ required! On top of performing the computations, that includes its own heap allocations and freeing, which the C++ code is still doing but our Julia tls method is avoiding at the cost of increasing the total amount of memory needed through creating task local caches.
I'll leave further possible optimizations to future work. One last thing we'll look at here are some LinxuPerf summaries:
using LinuxPerf
function perf(f::F, Bs, As, testrange) where {F}
GC.gc(); @time @pstats "cpu-cycles,(instructions,branch-instructions,branch-misses),(task-clock,context-switches,cpu-migrations,page-faults),(L1-dcache-load-misses,L1-dcache-loads,L1-icache-load-misses),(dTLB-load-misses,dTLB-loads),(iTLB-load-misses,iTLB-loads)" begin
do_multithreaded_work!(f, Bs, As, testrange)
end
end
precomprange = range(0.001, stop = 6.0, length=1<<8);
perf(expm_tls!, Bs, As, precomprange);
perf(gccexpm!, Bs, As, precomprange);
perf(clangexpm!, Bs, As, precomprange);
perf(expm_tls!, Bs, As, testrange)0.249814 seconds (434.07 k allocations: 53.308 MiB, 81.57% compilation ti
me)
0.019731 seconds (14.84 k allocations: 8.978 MiB)
0.018594 seconds (14.84 k allocations: 8.978 MiB)
2.886201 seconds (48.92 M allocations: 3.061 GiB, 9.13% gc time)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
╶ cpu-cycles 2.40e+11 60.0% # 2.6 cycles per ns
┌ instructions 2.39e+11 60.0% # 1.0 insns per cycle
│ branch-instructions 1.81e+10 60.0% # 7.6% of insns
└ branch-misses 8.27e+08 60.0% # 4.6% of branch insns
┌ task-clock 9.36e+10 100.0% # 93.6 s
│ context-switches 0.00e+00 100.0%
│ cpu-migrations 0.00e+00 100.0%
└ page-faults 7.30e+01 100.0%
┌ L1-dcache-load-misses 1.97e+09 20.0% # 2.5% of dcache loads
│ L1-dcache-loads 7.79e+10 20.0%
└ L1-icache-load-misses 2.02e+09 20.0%
┌ dTLB-load-misses 1.67e+07 20.0% # 0.0% of dTLB loads
└ dTLB-loads 7.80e+10 20.0%
┌ iTLB-load-misses 1.46e+07 40.0% # 23.9% of iTLB loads
└ iTLB-loads 6.12e+07 40.0%
aggregated from 53 threads
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━perf(clangexpm!, Bs, As, testrange)0.813010 seconds (406.52 k allocations: 938.334 MiB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
╶ cpu-cycles 1.10e+11 59.9% # 3.8 cycles per ns
┌ instructions 1.15e+11 60.0% # 1.0 insns per cycle
│ branch-instructions 6.44e+09 60.0% # 5.6% of insns
└ branch-misses 7.81e+08 60.0% # 12.1% of branch insns
┌ task-clock 2.87e+10 100.0% # 28.7 s
│ context-switches 0.00e+00 100.0%
│ cpu-migrations 0.00e+00 100.0%
└ page-faults 9.40e+01 100.0%
┌ L1-dcache-load-misses 1.59e+09 20.0% # 4.9% of dcache loads
│ L1-dcache-loads 3.26e+10 20.0%
└ L1-icache-load-misses 2.92e+08 20.0%
┌ dTLB-load-misses 4.53e+05 20.0% # 0.0% of dTLB loads
└ dTLB-loads 3.26e+10 20.0%
┌ iTLB-load-misses 3.90e+05 40.0% # 2.9% of iTLB loads
└ iTLB-loads 1.36e+07 40.0%
aggregated from 36 threads
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━perf(gccexpm!, Bs, As, testrange)0.882942 seconds (406.52 k allocations: 938.334 MiB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
╶ cpu-cycles 1.20e+11 60.0% # 3.8 cycles per ns
┌ instructions 1.41e+11 60.0% # 1.2 insns per cycle
│ branch-instructions 8.30e+09 60.0% # 5.9% of insns
└ branch-misses 7.24e+08 60.0% # 8.7% of branch insns
┌ task-clock 3.13e+10 100.0% # 31.3 s
│ context-switches 0.00e+00 100.0%
│ cpu-migrations 0.00e+00 100.0%
└ page-faults 0.00e+00 100.0%
┌ L1-dcache-load-misses 1.68e+09 20.0% # 4.0% of dcache loads
│ L1-dcache-loads 4.19e+10 20.0%
└ L1-icache-load-misses 2.56e+08 20.0%
┌ dTLB-load-misses 2.64e+05 20.0% # 0.0% of dTLB loads
└ dTLB-loads 4.19e+10 20.0%
┌ iTLB-load-misses 1.16e+05 39.9% # 0.9% of iTLB loads
└ iTLB-loads 1.31e+07 39.9%
aggregated from 36 threads
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━The most striking differences here are in the number of instructions, and in the number of icache-load misses, about one per two-hundred clock cycles for Julia, versus about one per five-hundred for the C++ implementations.
With this in mind, the next optimization to try would be ForwardDiff#570, a PR which adds explicit SIMD accumulation of partials. Trying it on Julia master, I get:
julia> GC.gc(); @time do_multithreaded_work!(expm_tls!, Bs, As, testrange);
1.274884 seconds (21.29 M allocations: 728.857 MiB, 6.78% gc time)
julia> GC.gc(); @time do_multithreaded_work!(clangexpm!, Bs, As, testrange);
0.788763 seconds (8.41 k allocations: 4.532 MiB)
julia> GC.gc(); @time do_multithreaded_work!(gccexpm!, Bs, As, testrange);
0.858725 seconds (8.41 k allocations: 4.532 MiB)Which is finally within 2x of the C++ code.
These results were obtained using
using InteractiveUtils: versioninfo
versioninfo()Julia Version 1.9.4
Commit 8e5136fa29 (2023-11-14 08:46 UTC)
Build Info:
Note: This is an unofficial build, please report bugs to the project
responsible for this build and not to the Julia project unless you can
reproduce the issue using official builds available at https://julialan
g.org/downloads
Platform Info:
OS: Linux (x86_64-generic-linux)
CPU: 36 × Intel(R) Core(TM) i9-10980XE CPU @ 3.00GHz
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-14.0.6 (ORCJIT, cascadelake)
Threads: 36 on 36 virtual cores
Environment:
LD_LIBRARY_PATH = /usr/local/lib/x86_64-unknown-linux-gnu/:/usr/local/lib
/:/usr/local/lib/x86_64-unknown-linux-gnu/:/usr/local/lib/
JULIA_NUM_THREADS = 36
JULIA_PATH = @.
LD_UN_PATH = /usr/local/lib/x86_64-unknown-linux-gnu/:/usr/local/lib/To build the notebook, you need Clang 17 installed on the path and Weave.
using Weave
weave("bench_notebook.jmd", informat="markdown", doctype="github")